Introduction
Here we consider a series of questions related to the sun and its properties. Topics for consideration include the luminosity of the sun and furthest distance at which a similar star could be seen, and what this distance is in various units of measurement. We are addressing questions 5-8 from the worksheet.
Solutions
Question: Given the that eye must receive 10 photons in order to see something, how far away would a solar twin have to be for it to be barely visible from Earth?
We will need to make a few assumptions for this problem:
· The “read rate” of the eye (in what length of time the photons must arrive to be visible) is 1/30 second (this is the frame rate for most movies)
· The sun emits light at 500 nm.
· The human eye has a surface area of .0625 square centimeters that can receive photons.
· The sun’s luminosity is 4*1033 ergs.
Using this assumption, we can calculate the minimum flux needed to see something. If the sun emits light at 500 nm, we can calculate the energy of 10 photons, and then find what this energy implies for the flux needed to see something.
E=hv and c=vl
3*1010= v*500*10-7
v=6*1014
E=(6.6*10-27)( 6*1014)
E=3.96*10-12
This is the energy for one photon. So, the energy for ten photons is 3.96*10-11 ergs. Also, if we want to find the minimum flux that would bring this energy to the eye, we must consider the surface area of the eye.
Minimum flux = (3.96*10-11 ergs)/(.0625 cm2)
Flux = 6.336*10-10 ergs/ cm2
Now, we have the minimum flux that the eye needs to see something. If we find the distance such that a star with the sun’s luminosity will have this flux at Earth, we will have our answer.
Flux=(luminosity)/(area)
What we can take this equation to mean for this problem is that given the luminosity of the sun, if we divide it by the surface area of the sphere with radius r, we will get the flux at some point r away from the sun. We can do this because photons are emitted isotropically from the sun. Now, in a previous problem on this worksheet (go see Iryna’s blog for the solution to that problem!), we found the luminosity of the sun to be roughly 4*1033 ergs. So:
6.336*10-10 ergs/ cm2 = (4*1033 ergs)/(4p(distance in cm)2)
Distance = 7.087*1020 cm
We can find this in AU (again, this is based on the answer to a previous problem! See Iryna’s post for details…):
7.087*1020 cm * (1 AU)/(1.5*1013cm) = x AU
X = 4.7*107 AU
For fun, let’s convert to lightyears.
4.7*107 AU * (8 lightminutes/1 AU)*(1 hour/60 minutes)*(1 day/24 hours)*(1 year/365 days) =715 lightyears
So, the farthest star we could see is 4.7*107 AU away. This is about 715 lightyears.
Question: The assumption in the last problem that all light from the sun is received at 500 nm is incorrect. In fact, light is processed by the eye at a “passband” of 450-600nm. Given this, how does the farthest distance at which a sun-strength star can be seen change?
Knowledge from earlier in the problem set and assumptions that we will use for this problem include:
· The “read rate” of the eye (in what length of time the photons must arrive to be visible) is 1/30 second (this is the frame rate for most movies)
· The sun emits light from 450 to 600 nm – however, not necessarily equally at all wavelengths.
· The human eye has a surface area of .0625 square centimeters that can receive photons.
· The sun’s luminosity is 4*1033 ergs.
No longer can we use the equations used in the previous problem, since now we have a band of wavelengths to consider. Instead, we can consider the equation for energy per wavelength, which was derived in a previous problem set:
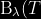=\frac{2hc^{^{2}}}{\lambda%20^{5}}\frac{1}{{e^{\frac{hc}{\lambda%20kT}-1}}})
To make this solvable, we will use a Taylor expansion around our e term. If we integrate this expression, from 450nm to 600nm:
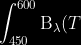=\frac{2hc^{^{2}}}{\lambda%20^{5}}\frac{1}{{\frac{hc}{\lambda%20kT}}}dT)
The answer to this integral is 1.01*10-10. We can use as the total energy for all wavelengths. Then, we divide this by 150 to get the energy for one photon – an average photon. This value is 6.7*10-13. Then, we can multiply this by 10 to get the energy for ten photons, which is 6.7*10-12. Then, we can use this to find the distance the star would need to be.
Minimum flux = (6.7*10-12 ergs)/(.0625 cm2)
Flux = 1.077*10-10 ergs/ cm2
Using this flux, we can use the same method as in the previous problem.
Flux=(luminosity)/(area)
1.077*10-10 ergs/ cm2 = (4*1033 ergs)/(4p(distance in cm)2)
Distance = 1.72*1021 cm
We can find this in AU:
1.72*1021 cm * (1 AU)/(1.5*1013cm) = x AU
X = 1.14*108 AU
Again, for fun:
1.14*108 AU * (8 lightminutes/1 AU)*(1 hour/60 minutes)*(1 day/24 hours)*(1 year/365 days) =1735 lightyears
So, a more accurate measurement of the farthest star we could see is 1.14*108 AU away. This is 1735 lightyears.
Question: How far away is this star in centimeters?
We actually found this figure mid-way through our calculation in the previous problem, so lifting that answer gives us:
Distance farthest star we can see is from Earth: 1.72*1021 cm
Question: How far is this is parsecs?
Knowledge from earlier in the problem set and assumptions that we will use for this problem include:
· The farthest a star of sun luminosity could be from the Earth for us to see it is 1.14*108 AU
First, we should find the distance of a parsec. A parsec is, as the problem explains, the distance from Earth a star must be in order to have a parallax of 1 arcsecond (recall, 1 arcsecond = 1/3600 degrees) from the sun.

Using the small angle approximation, and converting our 1/3600 into radians (p/648000)
tan(p/648000) = 1 AU / (x)
1/(p/648000)= 1/x
1 parsec = x =1 / (p/648000) = 2.06*105 AU
Now we know how many AU there are in a parsec, we can calculate how far the farthest star we can see is. Using the value for distance we previously calculated,
1.14*108 AU * (1 parsec/ 2.06*105 AU) = 5.52*102 parsecs = 552 parsecs
Conclusion
We have found that the farthest distance a star of sun luminosity could be from the Earth for us to still be able to see in with our naked eye is 1.14*108 AU. This is equivalent to 1.72*1021 cm, or 552 parsecs, or 1735 lightyears. Our preliminary estimate was 4.7*107 AU (which is about 715 lightyears), and we have also found the distance of a parsec (2.06*105 AU).
Acknowledgements
Thanks to Iryna Butsky for significant help on these problems! See her blog for problems 1-4.





 The VLA looks small compared to the Very Large Baseline Array (VLBA), however. VLBA is a system of similar radio antennas, also 25 meters in diameter, which are spread across the whole United States. To the left, the locations of the dishes are shown - image from the NRAO website (you can also go there for more information):
The VLA looks small compared to the Very Large Baseline Array (VLBA), however. VLBA is a system of similar radio antennas, also 25 meters in diameter, which are spread across the whole United States. To the left, the locations of the dishes are shown - image from the NRAO website (you can also go there for more information): 